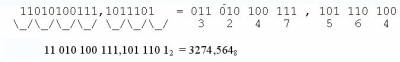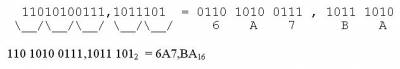Помощь студентам
Каталог статей
| Главная » Статьи » Учебное пособие. » Арифметические основы ЭВМ |
Перевод чисел из одной системы счисления в другую. Способ перевода зависит от того, в какой системе производятся арифметические операции. Для человека это десятичная система счисления. Перевод чисел из любой системы в десятичную. Производится по формуле представления чисел в позиционной системе счисления A(q) = anqn + an-1qn-1 + . . . + a1q1 + a0q0 + a-1q-1 + . . . + a-mq-m Примеры:
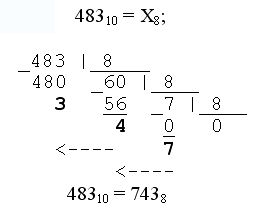
7438 = Х10 = 7·82 + 4·81 + 3·80 = 7·64 + 4·8 + 3·1 = 448 + 32 +3 = 48310
101001,112 = Х10 = 1·25 + 0·24 + 1·23 + 0·22 + 0·21 + 1·20 + 1·2-1 + 1·2-2 = = 32 + 0 + 8 + 0 + 0 + 1 + 1/2 + 1/4 = 41,7510 С5Е,416 = Х10 = 12·162 + 5·161 + 14·160 + 4·16-1 =
= 12·256 + 5·16 + 14·1 + 4·(1/16) = 3072 + 80 + 14 + 1/4 =
= 3166,2510
(С16 = 1210, Е16 = 1410)
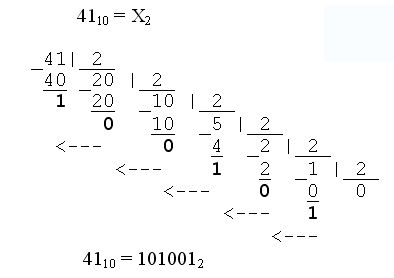
Перевод чисел из десятичной в любую систему счисления. Производится методом деления/умножения отдельно для целой и отдельно для дробной части десятичного числа. Для перевода целого числа (целой части) оно делится нацело на основание новой системы счисления и находится остаток от деления. Операция повторяется с каждым полученным частным до тех пор, пока результат не достигнет нуля. Остатки от деления, записанные в обратной последовательности, дают требуемое число в новой системе счисления. Примеры:
   Для перевода дробной части (дроби) она умножается на основание новой системы счисления. Операция умножения повторяется с дробной частью произведения до тех пор, пока не получим нулевую дробную часть или не достигнем заданной точности. Целые части произведений, записанные в прямой последовательности, дают искомую дробь в новой системе счисления. Примеры:
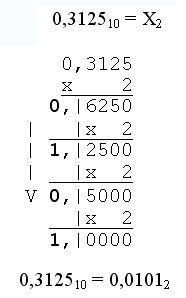 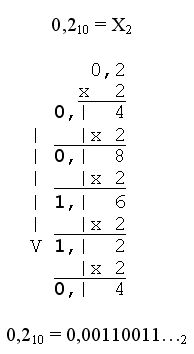 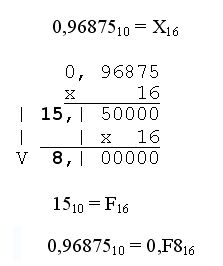 Внимание! При переводе правильных дробей из одной системы в другую могут получаться бесконечные дроби!
Перевод восьмеричных и шестнадцатиричных чисел в двоичные и наоборот.
Применение этих систем счисления связано с гораздо более короткой записью чисел при простоте перевода в двоичную систему и наоборот. 8 = 81 =23, поэтому 8 восьмеричных цифр полностью используют все возможные комбинации трех двоичных разрядов (триад). Для перевода восьмеричного числа в двоичное каждая его цифра заменяется полной (с начальными нулями) двоичной триадой. 6302,158 = Х2; ( 68 = 1102 38 = 0112 08 = 0002 28 = 0102 18 = 0012 58 = 1012 ) 6302,158 = 110 011 000 010 , 001 1012 Для перевода двоичного числа в восьмеричное оно разбивается на полные триады влево/вправо от запятой, после чего каждая триада заменяется восьмеричной цифрой: Т.к. 16 = 24, перевод чисел осуществляется аналогично, только шестнадцатиричная цифра заменяется полной тетрадой (четыре двоичных разряда). А19,С516 = Х2; ( А16 = 10102 116 = 00012 916 = 10012 С16 = 11002 516 = 01012 ) А19,С516 = 1010 0001 1001 , 1100 01012 Двоично-десятичная система (Д-коды). При работе ЭВМ производится перевод чисел из десятичной системы в двоичную и наоборот, что занимает машинное время. При решении научных задач это время несущественно (данных мало, а вычисления большие и сложные), а при решении социально-экономических – наоборот (огромное количество данных при простых расчетах). Для решения задач с большим количеством данных была разработана двоично-десятичная арифметика, которая требует больше времени на вычисления, чем двоичная, но значительно сокращает время на ввод и преобразование данных. В двоично-десятичной системе каждая десятичная цифра числа заменяется полной двоичной тетрадой (Д-кодом). Т.к. тетрадой можно записать 16 цифр, а в десятичной системе их 10, возможно огромное количество вариантов Д-кодов. На практике применимы те варианты Д-кодов, в которых для каждой цифры вес (численное содержание) каждого двоичного разряда не меняется. Наибольшее распространение получили Д-коды 8421 (нормальные двоичные веса), 8421+3, 8421+6, 2421, и др.. Примеры: 510 = 0101(8421) = 0·8 + 1·4 + 0·2 + 1·1 = 510 510 = 1000(8421+3) = 1·8 + 0·4 + 0·2 + 0·1 = (5 + 3)10 (код с избытком 3 – каждая десятичная цифра записывается увеличенным на 3 двоичным числом 010 = 0011(8421+3)) 510 = 1011(2421) = 1·2 + 0·4 + 1·2 + 1·1 = 510 Т.к. в любом Д-коде используется только 10 комбинаций тетрады из 16, существуют 6 запрещенных комбинаций, которые применять нельзя. Двоично-десятичные цифры, даже при использовании кода 8421, отличаются от изображения этих же чисел двоичным числом. 4110 = 1010012 = 0100 0001(8421) 25510 = 111111112 = 0010 0101 0101(8421) | |
| Категория: Арифметические основы ЭВМ | Добавил: logic-help (26.10.2008) | |
| Просмотров: 20799 | Комментарии: 1 | Рейтинг: 5.0/3 | |
| Всего комментариев: 1 | ||
| ||
Приветствую Вас Гость
Категории каталога | ||
|---|---|---|
|
Форма входа |
|---|
Поиск |
|---|
|
|
Друзья сайта |
|---|
Статистика |
|---|
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
Наш опрос |
|---|